PENGERTIAN MATRIKS RUMUS & DETERMINAN

 

Pengertian Matriks

disusun oleh,               NAMA                                : MUHAMMAD AFWAN FAJRI

                                    NIM                                    : 202031003

                                    FAKULTAS                         : TELEMATIKA ENERGI

                                    PERGURUAN TINGGI      : INSTITUT TEKNOLOGI PLN

                                    PRODI                                : S1 TEKNIK INFORMATIKA

                                    KELAS                               : A

                                    MATA KULIAH                 : ALJABAR LINIER                                                        


Matriks merupakan kumpulan bilangan, simbol, atau ekspresi dengan bentuk persegi panjang, sesuai baris dan kolom. Ordo matriks menunjukkan banyaknya baris dan kolom dalam matriks. Transpose matriks adalah bentuk operasi matriks di mana susunan baris diubah jadi kolom dan kolom diubah jadi baris. Matriks sama adalah matriks yang punya ordo-ordo yang sama dan tiap elemennya terletak pada baris dan kolom yang sama.


 Playlist di youtube (VLOG) : 

1. https://youtu.be/qEWyLiE4g-8 (Matriks)

2. https://youtu.be/TNeaYMyv0lc (Determinan Baris dan Kolom)

3. https://youtu.be/pV7pzSIGFrw (Determinan Metode CHIO)

4. https://youtu.be/fr53VpBf2Ho (Determinan Metode Crout dan Dolittle)

5. https://youtu.be/174GCj9MHpc  (Invers Matriks Metode Adjoin)

6. https://youtu.be/exhQWGZN0Io ( Gauss Jordan)

Matriks adalah kumpulan bilangan, simbol, atau ekspresi yang disusun membentuk persegi panjang berdasarkan baris dan kolom. Notasi matriks dinyatakan dalam huruf kapital. Berikut ini contoh penulisan matriks.

Matriks D di atas memiliki sembilan elemen, yaitu a–i.Letak elemen dinyatakan dalam fungsi xp,qdi mana p menunjukkan baris, sedangkan q menunjukkan kolom, contohnya x2,3= f; x3,1=g; dan x2,2= e. Baris merupakan bagian matriks yang mengarah horizontal, sedangkan kolom merupakan bagian matriks yang mengarah vertikal.

Contoh mudah matriks dapat kamu lihat dalam ilustrasi di bawah ini:

matriks dalam matematika

Ilustrasi di atas dapat kamu baca seperti ini: a11 dibaca baris ke-1 dan kolom ke-1; a12 dibaca baris ke-1 dan kolom ke-2; atau amn yang berarti baris ke-m dan kolom ke-n. Banyaknya baris dan kolom dalam matriks disebut dengan ordo. Urutan yang perlu diingat adalah baris kemudian kolom. Matriks dalam ilustrasi di bawah ini memiliki ordo 2x3, karena memiliki dua baris dan tiga kolom.

Untuk mengetahui matriks dalam matematika lebih dalam, ada beberapa jenis matriks yang perlu kamu ketahui, Squad. Jenis-jenisnya adalah:

1. Matriks nol             : matriks yang semua elemennya adalah nol.

2. Matriks baris         : matriks yang hanya memiliki satu baris.

3. Matriks kolom      : matriks yang hanya memiliki satu kolom.

4. Matriks persegi    : matriks yang memiliki jumlah baris dan kolom yang sama.

5. Matriks identitas : matriks konstanta dengan elemen diagonal utama adalah 1.



Ordo Matriks


Ordo atau ukuran matriks menunjukkan banyaknya baris dan kolom di dalam matriks. Ordo biasa dinotasikan sebagai  ∑ baris x kolom. Perhatikan contoh berikut.

Transpose Matriks

Transpose matriks merupakan bentuk operasi matriks di mana susunan baris diubah menjadi kolom, sedangkan bagian kolom diubah menjadi baris. Baris ke-p diubah menjadi kolom ke-p atau kolom ke-q diubah menjadi baris ke-q. Jika matriks D di atas dijadikan transpose matriks D, notasi yang digunakan adalah DT. Untuk lebih jelasnya, perhatikan contoh berikut.

Berdasarkan transpose matriks di atas, kalian bisa melihat bahwa elemen baris ke-1, yaitu 1, 2, 3, dituliskan pada kolom ke-1, elemen baris ke-2, yaitu 4, 5, 6, dituliskan pada kolom ke-2, dan begitu seterusnya. Dengan demikian, transpose matriks bisa mengubah ordo matriks jika jumlah baris dan kolomnya tidak sama.


Matriks Sama


Suatu matriks dikatakan sama jika matriks-matriks tersebut memiliki ordo yang sama dan setiap elemennya terletak pada baris dan kolom yang sama. Jika suatu matriks sama, otomatis setiap elemen yang seletak nilainya sama. Perhatikan contoh soal berikut.

Contoh Soal 1

Diketahui dua matriks sebagai berikut.

Tentukan nilai dari a, b,c, dan d!
Pembahasan:
Untuk mencari nilai a, b,c, dan d, kalian harus tahu bahwa matriks D = E, sehingga elemen seletak nilainya pasti sama.

Dari perhitungan di atas, diperoleh nilai a= 1, b = 6, c= 0, dan d= 9.
Jadi, nilai a, b,c, dan d berturut-turut adalah 1, 6, 0, dan 9.


Operasi Antarmatriks


Layaknya bilangan, matriks juga bisa dioperasikan seperti penjumlahan, pengurangan, perkalian angka dengan matriks, maupun perkalian antarmatriks.

1. Penjumlahan dan pengurangan matriks

Penjumlahan dan pengurangan matriks hanya bisa dilakukan jika ordonya sama, misalnya matriks 2 × 2 dikurangkan dengan matriks 2 × 2 lainnya. Elemen yang dijumlahkan atau dikurangkan harus seletak, artinya posisi atau letaknya sama. Perhatikan contoh berikut.

Berdasarkan contoh di atas, terlihat bahwa penjumlahan atau pengurangan matriks tidak mengakibatkan perubahan ordo.

2. Perkalian angka dengan matriks

Semua matriks bisa dikalikan dengan konstanta atau bilangan berapapun. Jika dikalikan dengan suatu konstanta atau bilangan, semua elemen di dalam matriks tersebut harus dikalikan satu per satu dengan konstanta yang dimaksud. Contohnya sebagai berikut.

Berdasarkan hasil di atas, ternyata perkalian antara konstanta dan matriks tidak akan mengubah ordo matriks tersebut.

3. Perkalian antara matriks dan matriks

Jika dibandingkan operasi matriks sebelumnya, perkalian antara matriks dan matriks ini terbilang lebih rumit. Untuk mengalikan antara matriks dan matriks, kalian harus mengalikan seluruh elemen tiap baris ke-pdengan kolom ke-­p, lalu hasilnya dijumlahkan pada baris yang sama. Misalnya diketahui perkalian matriks sebagai berikut.

Contoh mengoperasikan perkalian antara dua matriks di atas adalah sebagai berikut.
 

Pembahasan:

Hal yang harus diingat dari perkalian matriks adalah sifat perkalian matriks tidak berlaku bolak-balik atau  AB ≠ BA.
Agar kalian semakin paham dengan pembahasan matriks ini, perhatikan contoh soal berikut.

Contoh Soal 2


Pembahasan:
Sebelum menyelesaikan soal di atas, kalian jabarkan kembali persamaannya, yaitu sebagai berikut.

Selanjutnya, tentukan nilai x dan y berdasarkan nilai elemen seletak.

Diperoleh nilai x= 2 dan y= 4. Dengan demikian, x+ 2xy+ y= 2 + 2(2)(4) + 4 = 22.
Jadi, nilai x+ 2xy+ y= 22.

Contoh soal 3

Tentukan nilai 2a2+ b– c  yang memenuhi persamaan matriks berikut.

Pembahasan:
Untuk menentukan nilai 2a2+ b– c, kalian harus mengalikan matriks-matriks di sisi kiri terlebih dahulu.

Dari persamaan di atas, diperoleh:
Baris ke-2, kolom ke-2

Baris ke-1, kolom ke-2

Baris ke-1, kolom ke-1

Dengan demikian, nilai 2a2+ b– c= 2(3)2+ (-3) – 1 = 14.
Jadi, nilai 2a2+ b– c= 14.

DETERMINAN MATRIKS

Fungsi determinan matrik bujur sangkar A dinyatakan dengan det(A)=|A|, didefinisikan sebagai jumlahan hasil kali elementer elemen-elemen bertanda A.Sehingga bentuknya terlihat seperti persegi. Cara menentukan determinan matriks akan berbeda pada tiap ordo.Dengan ukuran 2×2, 2×3, 3×3, 4×4

Determinan Matriks Berordo 2 x 2

 Contoh matriks dengan ordo 2 x 2  adalah seperti ini:

Matriks A merupakan matriks dengan ordo 2 × 2 memiliki elemen a dan d yang terletak pada diagonal utama, sedangkan b dan c terletak pada diagonal kedua. Nilai determinan A, disimbolkan dengan [A], merupakan suatu bilangan yang diperoleh dengan cara mengurangkan hasil kali elemen-elemen pada diagonal utama dengan hasil kali elemen-elemen diagonal kedua.

Rumus yang dapat kamu gunakan adalah:

Det (A) = |A| = ad – bc

Untuk bisa memahami rumus ini dengan lebih baik, mari kita lihat contoh soal berikut ini.

Contoh Soal Determinan Matriks Berordo 2 x 2

Untuk bisa lebih memahami determinan matriks, mari kita perhatikan soal determinan matriks berordo 2 x 2 berikut ini:

1. Tentukan determinan dari matriks berikut ini!

contoh cara mencari determinan matriks ordo 2x2

Solusi:

Bila kita perhatikan matriks di atas, kita dapat langsung menghitung nilai determinan dengan rumus yang telah kita ketahui.

Det (A) = |A| = ad – bc

|A| = (5 x 6) – (2 x 4)

|A| = 30 – 8

|A| = 22

 

2. Berapakah determinan dari matriks di bawah ini?

contoh cara mencari determinan matriks ordo 2x2

Solusi:

Sama dengan soal yang pertama, kita bisa menggunakan rumus untuk bisa menyelesaikannya.

Det (A) = |A| = ad – bc

|A| = (7 x 3) – (2 x 8)

|A| = 21 – 16

|A| = 5

 

Determinan Matriks Berordo 3 x 3

Matriks berordo 3×3 adalah matriks berbentuk persegi dengan banyak kolom dan baris sama yaitu tiga. Bentuk umum matriks berordo 3×3 sebagai berikut:

contoh cara mencari determinan matriks ordo 3x3

Untuk menghitung determinan matriks berordo 3×3, kamu bisa menggunakan aturan Sarrus. Gambar di bawah ini akan menunjukkan caranya dengan lebih jelas.

determinan matriks ordo 3x3

Sumber Gambar: idschool.net

Untuk bisa memahami cara ini dengan lebih baik, mari kita perhatikan beberapa contoh soal berikut ini.

Contoh Soal Determinan Matriks Berordo 3×3

Untuk dapat memahami determinan matriks berordo 3 x 3, ada beberapa soal yang akan bisa menambah pemahaman kamu mengenai hal ini.

1. Tentukan determinan dari matriks di bawah ini!

contoh cara mencari determinan matriks ordo 3x3

Solusi:

Untuk menyelesaikan soal di atas, maka kita akan menggunakan aturan Sarrus.

|A| = aei + bfg + cdh – ceg – afh – bdi

|A| = (1x5x6) + (4x2x1) + (1x2x3) – (1x5x1) – (1x2x3) – (4x2x6)

|A| = 30 + 8 + 6 – 5 – 6 – 48

|A| = -15

 

2. Berapakah determinan dari matriks di bawah ini?

contoh cara mencari determinan matriks ordo 3x3

Solusi:

Untuk menyelesaikan soal di atas, maka kita akan menggunakan aturan Sarrus.

|A| = aei + bfg + cdh – ceg – afh – bdi

|A| = (2x5x1) + (4x2x2) + (1x3x3) – (1x5x2) – (2x2x3) – (4x3x1)

|A| = 10 + 16 + 9 – 10 – 12 – 12

|A| = 1


METODE EKSPANSI LAPLACE

Pengertian

Metode Laplace adalah suatu teknik untuk menyederhanakan permasalahan dalam suatu sistem yang mengandung masukan dan keluaran, dengan melakukan transformasi dari suatu domain pengamatan ke domain pengamatan yang lain

DETERMINAN METODE EKSPANSI LAPLACE

Andaikan, A=[aij] (nxn) adalah matrik bujur sangkar berordo (nxn), dan Cij = (-1)i+j Mij adalah kofaktor elemen matrik A baris ke-i kolom ke-j.

Screenshot (18)

Cara menghitung determinan (A) dengan ekspansi kofaktor (Ordo 3×3)

Screenshot (20)

Cara menghitung determinan (A) dengan ekspansi kofaktor (Ordo 4×4)

Ekspansi kofaktor baris

screenshot-22-e1538749593725.png

Ekspansi kofaktor kolom

Screenshot (22)


DETERMINAN : METODE CHIO

Determinan merupakan suatu fungsi dari himpunan semua matriks persegi ke himpunan semua bilangan real. Determinan matriks A biasanya dinyatakan oleh |A| atau det(A). Terdapat beberapa metode yang digunakan untuk menentukan determinan matriks yaitu metode Sarrus, Ekspansi Kofaktor, dan Kondensasi (Penyusutan) CHIO. Kondensasi CHIO merupakan salah satu metode yang dapat digunakan dalam menentukan determinan matriks yang memiliki ordo n \times n dengan n \geq 3.
Kondensasi CHIO menyusutkan determinan matriks ordo n \times n menjadi ordo (n-1) \times (n-1) dan dikalikan dengan elemen a_{11}. Proses kondensasi ini berakhir pada determinan matriks ordo 2 \times 2. Tanpa mengurangi perumuman, dalam tulisan ini menggunakan matriks persegi dengan syarat elemen a_{11} \neq 0. Apabila nilai elemen a_{11} = 0 maka dilakukan proses operasi baris/kolom yaitu menukarkan baris/kolom pada determinan matriks untuk memperoleh a_{11} \neq 0.

Perhatikan untuk matrik dengan ordo 3 \times 3. Persamaan yang digunakan untuk metode CHIO ini sebagai berikut.

det(A) = \dfrac{1}{(a_{11})^{3-2}} \begin{vmatrix} \begin{vmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{vmatrix} & \begin{vmatrix} a_{11} & a_{13}\\ a_{21} & a_{23} \end{vmatrix}\\ &\\ \begin{vmatrix} a_{11} & a_{12}\\ a_{31} & a_{32} \end{vmatrix} & \begin{vmatrix} a_{11} & a_{13}\\ a_{31} & a_{33} \end{vmatrix} \end{vmatrix}

Selanjutnya untuk matrik dengan ordo 4 \times 4. Persamaan yang digunakan untuk metode CHIO ini sebagai berikut.

det(A) = \dfrac{1}{(a_{11})^{4-2}} \begin{vmatrix} \begin{vmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{vmatrix} & \begin{vmatrix} a_{11} & a_{13}\\ a_{21} & a_{23} \end{vmatrix} & \begin{vmatrix} a_{11} & a_{14}\\ a_{21} & a_{24} \end{vmatrix}\\ &&\\ \begin{vmatrix} a_{11} & a_{12}\\ a_{31} & a_{32} \end{vmatrix} & \begin{vmatrix} a_{11} & a_{13}\\ a_{31} & a_{33} \end{vmatrix} & \begin{vmatrix} a_{11} & a_{14}\\ a_{31} & a_{34} \end{vmatrix}\\ &&\\ \begin{vmatrix} a_{11} & a_{12}\\ a_{41} & a_{42} \end{vmatrix} & \begin{vmatrix} a_{11} & a_{13}\\ a_{41} & a_{43} \end{vmatrix} & \begin{vmatrix} a_{11} & a_{14}\\ a_{41} & a_{44} \end{vmatrix}\\ \end{vmatrix}

Apabila ukuran matriksnya diperluas atau diperumum menjadi n \times n, maka diperoleh persamaan untuk metode CHIO adalah sebagai berikut.

det(A) = \dfrac{1}{(a_{11})^{n-2}} \begin{vmatrix} \begin{vmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{vmatrix} & \begin{vmatrix} a_{11} & a_{13}\\ a_{21} & a_{23} \end{vmatrix} & \ldots & \begin{vmatrix} a_{11} & a_{1n}\\ a_{21} & a_{2n} \end{vmatrix}\\ &&&\\ \begin{vmatrix} a_{11} & a_{12}\\ a_{31} & a_{32} \end{vmatrix} & \begin{vmatrix} a_{11} & a_{13}\\ a_{31} & a_{33} \end{vmatrix} & \ldots & \begin{vmatrix} a_{11} & a_{1n}\\ a_{31} & a_{3n} \end{vmatrix}\\ &&&\\ \vdots & \vdots & \ddots & \vdots\\ \begin{vmatrix} a_{11} & a_{12}\\ a_{n1} & a_{n2} \end{vmatrix} & \begin{vmatrix} a_{11} & a_{13}\\ a_{n1} & a_{n3} \end{vmatrix} & \ldots & \begin{vmatrix} a_{11} & a_{1n}\\ a_{n1} & a_{nn} \end{vmatrix}\\ \end{vmatrix}

Contoh 1.

Hitung determinan matriks A = \begin{bmatrix} -2&1&4\\ 3&-5&2\\ 5&2&1 \end{bmatrix}.

Dengan menggunakan metode CHIO, maka didapat

det(A) = \dfrac{1}{(-2)^{3-2}} \begin{vmatrix} \begin{vmatrix} -2&1\\ 3&-5 \end{vmatrix} & \begin{vmatrix} -2&4\\ 3&2 \end{vmatrix}\\ &\\ \begin{vmatrix} -2&1\\ 5&2 \end{vmatrix} & \begin{vmatrix} -2&4\\ 5&1 \end{vmatrix} \end{vmatrix}

= \dfrac{1}{-2} \begin{vmatrix} (-5)(-2)-(3)(1) & (-2)(2)-(3)(4)\\ (-2)(2)-(1)(5) & (-2)(1)-(4)(5) \end{vmatrix}

= \dfrac{1}{-2} \begin{vmatrix} 7&-16\\ -9&-22 \end{vmatrix}

= \dfrac{1}{-2} (7 \cdot -22-(-16) \cdot -9)

= \dfrac{1}{-2} (-154-144)

= \dfrac{1}{-2} (-298)

= -149

Contoh 2.

Hitung determinan matriks B = \begin{bmatrix} 2&1&6&7\\ 3&2&4&5\\ 4&4&2&3\\ 5&6&1&4 \end{bmatrix}.

Dengan menggunakan metode CHIO, maka didapat

det(B) = \dfrac{1}{(2)^{4-2}} \begin{vmatrix} \begin{vmatrix} 2&1\\ 3&2 \end{vmatrix} & \begin{vmatrix} 2&6\\ 3&4 \end{vmatrix} & \begin{vmatrix} 2&7\\ 3&5 \end{vmatrix}\\ &&\\ \begin{vmatrix} 2&1\\ 4&4 \end{vmatrix} & \begin{vmatrix} 2&6\\ 4&2 \end{vmatrix} & \begin{vmatrix} 2&7\\ 4&3 \end{vmatrix}\\ &&\\ \begin{vmatrix} 2&1\\ 5&6 \end{vmatrix} & \begin{vmatrix} 2&6\\ 5&1 \end{vmatrix} & \begin{vmatrix} 2&7\\ 5&4 \end{vmatrix} \end{vmatrix}

= \dfrac{1}{2^2} \begin{vmatrix} (2)(2)-(3)(1) & (2)(4)-(3)(6) & (2)(5)-(3)(7)\\ (2)(4)-(1)(4) & (2)(2)-(4)(6) & (2)(3)-(7)(4)\\ (2)(6)-(1)(5) & (2)(1)-(6)(5) & (2)(4)-(7)(5) \end{vmatrix}

= \dfrac{1}{4} \begin{vmatrix} 1&-10&-11 \\ 4&-20&-22\\ 7&-28&-27 \end{vmatrix}

Misal C = \begin{vmatrix} 1&-10&-11 \\ 4&-20&-22\\ 7&-28&-27 \end{vmatrix}, diperoleh

det(C) = \dfrac{1}{1^{3-2}} \begin{vmatrix} \begin{vmatrix} 1&-10\\ 4&-20 \end{vmatrix} & \begin{vmatrix} 1&-11\\ 4&-22 \end{vmatrix}\\ &\\ \begin{vmatrix} 1&-10\\ 7&-28 \end{vmatrix} & \begin{vmatrix} 1&-11\\ 7&-27 \end{vmatrix} \end{vmatrix}

= \dfrac{1}{1} \begin{vmatrix} (1)(-20)-(4)(-10) & (1)(-22)-(-11)(4)\\ (1)(-28)-(-10)(7) & (1)(-27)-(-11)(7) \end{vmatrix}

= \begin{vmatrix} 20 & 22\\ 42 & 50 \end{vmatrix}

= (20 \cdot 50-22 \cdot 42

= 1000-924

= 76

Jadi,

det(B) = \dfrac{1}{4} det(C)

= \dfrac{1}{4} (76)

= 19



SIFAT SIFAT DETERMINAN

Sifat-sifat determinan matriks sangat bermanfaat ketika menghitung matriks-matriks dengan karakteristik khusus. Seperti matriks dengan elemen nol, matriks segitiga atas/bawah, dan matriks dengan baris sebanding.

Sifat Determinan

Dalam perhitungan hanya metode Sarrus yang digunakan, karena metode ini lebih mudah dibandingkan dua metode lainnya.

  1. Jika matriks A sembarang yang semua elemen dalam salah satu baris atau kolomnya adalah nol, maka determinan A = 0.

Contoh matriks 2×2

BarisKolom
\vspace{1pc}A= \begin{bmatrix} 3 &-1\\ 0& 0\end{bmatrix}\\ \vspace{1pc}\left|A\right|=3.0-(-1.0)=0\\ \vspace{1pc}B= \begin{bmatrix} 0 &-1\\ 0& 4\end{bmatrix}\\ \vspace{1pc}\left|B\right|=0.4-(-1.0)=0

Contoh matriks 3×3

BarisKolom
\vspace{1pc}C= \begin{bmatrix} 3 &-1 &2\\ 0& 0&0\\4 &-3&1\end{bmatrix}\\ \vspace{1pc}\left|C\right|=3.0.1+(-1).0.4+2.0.(-3)\\-(2.0.4+3.0.(-3)+(-1).0.1)=0\vspace{1pc}D= \begin{bmatrix} 3 &-1 &0\\ 5& 2&0\\4 &-3&0\end{bmatrix}\\ \vspace{1pc}\left|D\right|=3.2.0+(-1).0.4+0.5.(-3)\\-(0.2.4+3.0.(-3)+(-1).5.0)=0

2. Jika matriks A sembarang adalah matriks segitiga atas, matriks segitiga bawah, atau matriks diagonal, maka determinan A = hasil kali elemen diagonal utama.

Contoh matriks 2×2

Segitiga AtasSegitiga Bawah
\vspace{1pc}A= \begin{bmatrix} 3 &-1\\ 0& 2\end{bmatrix}\\ \vspace{1pc}\left|A\right|=3\times2=6\\ \vspace{1pc}B= \begin{bmatrix} 3 &0\\ 4& 2\end{bmatrix}\\ \vspace{1pc}\left|B\right|=3\times2=6
Diagonal
\vspace{1pc}C= \begin{bmatrix} 3 &0\\ 0& 2\end{bmatrix}\\ \vspace{1pc}\left|C\right|=3\times2=6

Contoh matriks 3×3

Segitiga AtasSegitiga Bawah
\vspace{1pc}D= \begin{bmatrix} 3 &-1 &2\\ 0& 2&6\\0 &0&4\end{bmatrix}\\ \vspace{1pc}\left|D\right|=3\times2\times4=24\vspace{1pc}E= \begin{bmatrix} 3 &0 &0\\ 5& 2&0\\1 &-3&4\end{bmatrix}\\ \vspace{1pc}\left|E\right|= 3\times2\times4=24
Diagonal
\vspace{1pc}F= \begin{bmatrix} 3 &0 &0\\ 0& 2&0\\0&0&4\end{bmatrix}\\ \vspace{1pc}\left|F\right|= 3\times2\times4=24

3. Jika matriks A’ adalah matriks yang diperoleh dari matriks A setelah salah satu baris/kolomnya dikalikan dengan konstanta k, maka determinan A’ = k x Det A.
Contoh matriks 2×2

Matriks A
\vspace{1pc}A= \begin{bmatrix} 3 &-1\\ 5& 2\end{bmatrix}\\ \vspace{1pc}\left|A\right|=3.2-(-1).5=11
A’ (Baris)A’ (Kolom)
\vspace{1pc}k=3\\ \vspace{1pc}Baris\;ke-1\\ \vspace{1pc}Rumus=3R1\\ \vspace{1pc} A'= \begin{bmatrix} 9 &-3\\ 5& 2\end{bmatrix}\\ \vspace{1pc}\left|A'\right|=9.2-(-3).5=33\\ \vspace{1pc}atau\\A'= k\times\left|A\right|=3\times11=33\vspace{1pc}k=3\\ \vspace{1pc}Kolom\;ke-2\\ \vspace{1pc}Rumus=3C2\\ \vspace{1pc} A'= \begin{bmatrix} 3 &-3\\ 5& 6\end{bmatrix}\\ \vspace{1pc}\left|A'\right|=3.6-(-3).5=33\\ \vspace{1pc}atau\\A'= k\times\left|A\right|=3\times11=33

Contoh matriks 3×3

Matriks B
\vspace{1pc}B= \begin{bmatrix} 3 &-1 &2\\ 5& 2&6\\1 &-3&4\end{bmatrix}\\ \vspace{1pc}\left|B\right|= 3.2.4+(-1).6.1+2.5.(-3)\\ \vspace{1pc}-(2.2.1+3.6.(-3)+(-1).5.4)\\ \vspace{1pc}\left|B\right|=24-6-30-(4-54-20)=58
B’ (Baris)
\vspace{1pc}k=2\\ \vspace{1pc}Baris\;ke-3\\ \vspace{1pc}Rumus=2R3\\ \vspace{1pc}B'= \begin{bmatrix} 3 &-1 &2\\ 5& 2&6\\2 &-6&8\end{bmatrix}\\ \vspace{1pc}\left|B'\right|=3.2.8+(-1).6.2+2.5.(-6)\\ \vspace{1pc}-(2.2.2+3.6.(-6)+(-1).5.8)\\ \vspace{1pc}\left|B'\right|=48-12-60-(8-108-40)=116
B’ (Kolom)
\vspace{1pc}k=2\\ \vspace{1pc}Kolom\;ke-2\\ \vspace{1pc}Rumus=2C2\\ \vspace{1pc}B'= \begin{bmatrix} 3 &-2 &2\\ 5& 4&6\\1 &-6&4\end{bmatrix}\\ \vspace{1pc}\left|B'\right|=3.4.4+(-2).6.1+2.5.(-6)\\ \vspace{1pc}-(2.4.1+3.6.(-6)+(-2).5.8)\\ \vspace{1pc}\left|B'\right|=48-12-60-(8-108-40)=116

4. Jika matriks A’ dihasilkan dari matriks A setelah dua baris/kolomnya ditukarkan, maka determinan A’ = – det A.

Contoh matriks 2×2

Matriks A
\vspace{1pc}A= \begin{bmatrix} 3 &-1\\ 5& 2\end{bmatrix}\\ \vspace{1pc}\left|A\right|=3.2-(-1).5=11
Tukar BarisTukar Kolom
\vspace{1pc}Rumus=R1\Leftrightarrow R2\\ \vspace{1pc} A'= \begin{bmatrix} 5 &2\\ 3& -1\end{bmatrix}\\ \vspace{1pc}\left|A'\right|=5.(-1)-2.3=-11\\ \vspace{1pc}atau\\ \left|A'\right|= -\left|A\right|=-(11)=-11\vspace{1pc}Rumus=C1\Leftrightarrow C2\\ \vspace{1pc} A'= \begin{bmatrix} -1 &3\\ 2& 5\end{bmatrix}\\ \vspace{1pc}\left|A'\right|=(-1).5-3.2=-11\\ \vspace{1pc}atau\\ \left|A'\right|= -\left|A\right|=-(11)=-11

Contoh matriks 3×3

Matriks B
\vspace{1pc}B= \begin{bmatrix} 3 &-1 &2\\ 5& 2&6\\1 &-3&4\end{bmatrix}\\ \vspace{1pc}\left|B\right|= 3.2.4+(-1).6.1+2.5.(-3)\\ \vspace{1pc}-(2.2.1+3.6.(-3)+(-1).5.4)\\ \vspace{1pc}\left|B\right|=24-6-30-(4-54-20)=58
Tukar Baris
\vspace{1pc}Rumus=R1\Leftrightarrow R3\\ \vspace{1pc}B'= \begin{bmatrix} 1 &-3&4\\ 5& 2&6\\3 &-1 &2\end{bmatrix}\\ \vspace{1pc}\left|B'\right|=1.2.2+(-3).6.3+4.5.(-1)\\ \vspace{1pc}-(4.2.3+1.6.(-1)+(-3).5.2)\\ \vspace{1pc}\left|B'\right|=4-54-20-(24-6-30)=-58\\ \vspace{1pc}\left|B'\right|=-\left|B\right|=-58
Tukar Kolom
\vspace{1pc}Rumus=C2\Leftrightarrow C3\\ \vspace{1pc}B'= \begin{bmatrix} 3 &2 &-1\\ 5& 6&2\\1 &4&-3\end{bmatrix}\\ \vspace{1pc}\left|B'\right|=(-3).6.3+2.2.1++(-1).5.4\\ \vspace{1pc}-((-1).6.1+3.2.4+2.5.(-3))\\ \vspace{1pc}\left|B'\right|=-54+4-20-(-6+24-30)=-58\\ \vspace{1pc}\left|B'\right|=-\left|B\right|=-58

5. Jika A’ adalah matriks yang dihasilkan dari matriks A setelah salah satu baris/kolomnya dikalikan dengan konstanta kemudian dijumlahkan/dikurangkan terhadap baris/kolom yang lainnya, maka determinan A’ = determinan A.

Matriks A
\vspace{1pc}A= \begin{bmatrix} 3 &-1\\ 5& 2\end{bmatrix}\\ \vspace{1pc}\left|A\right|=3.2-(-1).5=11
BarisKolom
\vspace{1pc}R1+2R2\mapsto R1\\ \vspace{1pc}A'= \begin{bmatrix} 13 &3\\ 5& 2\end{bmatrix}\\ \vspace{1pc}\left|A'\right|=13.2-3.5=11\vspace{1pc}C2-\frac{1}{3}C1\mapsto C2\\ \vspace{1pc}A'= \begin{bmatrix} 3 &-2\\ 5& \frac{1}{3}\end{bmatrix}\\ \vspace{1pc}\left|A'\right|=3.\frac{1}{3}-(-2).5=11

Contoh matriks 3×3

Matriks B
\vspace{1pc}B= \begin{bmatrix} 3 &-1 &2\\ 5& 2&6\\1 &-3&4\end{bmatrix}\\ \vspace{1pc}\left|B\right|= 3.2.4+(-1).6.1+2.5.(-3)\\ \vspace{1pc}-(2.2.1+3.6.(-3)+(-1).5.4)\\ \vspace{1pc}\left|B\right|=24-6-30-(4-54-20)=58
Baris
\vspace{1pc}R2-\frac{1}{3}R1\mapsto R2\\ \vspace{1pc}B'= \begin{bmatrix} 3 &-1 &2\\ 0& \frac{11}{3}&\frac{8}{3}\\1 &-3&4\end{bmatrix}\\ \vspace{1pc}\left|B'\right|=3.\frac{11}{3}.4+(-1).\frac{8}{3}.1+2.0.(-3)\\ \vspace{1pc}-(2.\frac{11}{3}.1+3.\frac{8}{3}.(-3)+(-1).0.4)\\ \vspace{1pc}\left|B'\right|=44+0-\frac{8}{3}-(\frac{22}{3}-24+0)=58
Kolom
\vspace{1pc}C1+2C3\mapsto C1\\ \vspace{1pc}B'= \begin{bmatrix} 3 &-1 &2\\ 5& 2&6\\1 &-3&4\end{bmatrix}\\ \vspace{1pc}\left|B'\right|=7.2.4+(-1).6.9+2.17.(-3)\\ \vspace{1pc}-(2.2.9+7.6.(-3)+(-1).17.4)\\ \vspace{1pc}\left|B'\right|=56-54-102-(36-126-68)=58

6. Jika sebuah matriks mempunyai dua baris yang elemen-elemennya sebanding, maka determinannya adalah nol.

 Dua Baris Sama
\vspace{1pc}A= \begin{bmatrix} 3 &-1\\ 3& -1\end{bmatrix}\\ \vspace{1pc}\left|A\right|=3.(-1)-(-1).3=0
Baris SebandingKolom Sebanding
\vspace{1pc}B= \begin{bmatrix} 3 &-1\\ -3& 1\end{bmatrix}\\ \vspace{1pc}\left|B\right|=3.(-1)-(-3).1=0\vspace{1pc}C= \begin{bmatrix} 3 &-1\\ 6& -2\end{bmatrix}\\ \vspace{1pc}\left|C\right|=3.(-2)-(-1).6=0

Contoh matriks 3×3

Dua Baris Sama
\vspace{1pc}R1=R3\\ \vspace{1pc}D=\begin{bmatrix} 3 &-1 &2\\ 5& 2&6\\3 &-1 &2\end{bmatrix}\\ \vspace{1pc}\left|D\right|= 3.2.2+(-1).6.3+2.5.(-1)\\ \vspace{1pc}-(2.2.3+3.6.(-1)+(-1).5.2)\\ \vspace{1pc}\left|D\right|=12-18-10-(12-18-10)=0
Baris Sebanding
\vspace{1pc}R2\;sebanding\;R3\\ \vspace{1pc}E= \begin{bmatrix} 3 &-1 &2\\ 2& -6&8\\1 &-3&4\end{bmatrix}\\ \vspace{1pc}\left|E\right|=3.(-6).4+(-1).8.1+2.2.(-3)\\ \vspace{1pc}-(2.(-6).1+3.8.(-3)+(-1).2.4)\\ \vspace{1pc}\left|E\right|=-72-8-12-(-12-72-8)=0
Kolom Sebanding
\vspace{1pc}C1\;sebanding\;C2\\ \vspace{1pc}F= \begin{bmatrix} 2 &-1 &2\\ -4& 2&6\\6 &-3&4\end{bmatrix}\\ \vspace{1pc}\left|F\right|=2.2.4+(-1).6.6+2.(-4).(-3)\\ \vspace{1pc}-(2.2.6+2.6.(-3)+(-1).(-4).4)\\ \vspace{1pc}\left|F\right|=16-36+24-(24-36+16)=0

7. Suatu matriks nilai determinannya tidak akan berubah jika barisnya dijadikan kolom.

Dengan kata lain determinan matriks asal sama dengan determinan matriks hasil transpose.

Contoh matriks 2×2

Matriks ATranspose A
\vspace{1pc}A= \begin{bmatrix} 3 &-1\\ 5& 2\end{bmatrix}\\ \vspace{1pc}\left|A\right|=3.2-(-1).5=11\vspace{1pc}A^T= \begin{bmatrix} 3 &5\\ -1& 2\end{bmatrix}\\ \vspace{1pc}\left|A^T\right|=3.2-5.(-1)=11

Contoh matriks 3×3

Matriks B
\vspace{1pc}B= \begin{bmatrix} 3 &-1 &2\\ 5& 2&6\\1 &-3&4\end{bmatrix}\\ \vspace{1pc}\left|B\right|= 3.2.4+(-1).6.1+2.5.(-3)\\ \vspace{1pc}-(2.2.1+3.6.(-3)+(-1).5.4)\\ \vspace{1pc}\left|B\right|=24-6-30-(4-54-20)=58
Baris Sebanding
\vspace{1pc}B^T= \begin{bmatrix} 3 &5 &1\\ -1& 2&-3\\2 &6&4\end{bmatrix}\\ \vspace{1pc}\left|B^T\right|= 3.2.4+5.(-3).2+1.(-1).6\\ \vspace{1pc}-(1.2.2+3.(-3).6+5.(-1).4)\\ \vspace{1pc}\left|B^T\right|=24-30-6-(4-54-20)=58

DEKOMPOSISI MATRIK DAN DETERMINAN

Matrik bujur sangkar A dikatakan dapat didekomposisi, jika terdapat matrik segitiga bawah L dan matrik segitiga atas U sedemikian rupa sehingga :

               A = LU

Akibatnya :

          det(A) = det(L) det (U)

Det(A) = det(L) det(U)

Dalam menghitung dekomposisi matriks ada beberapa metode, diantaranya:

  1. Metode crout, metode ini digunakan untuk mendekomposisi matriks yang menghasilkan elemen diagonal utama dari matriks segitiga atas U adalah satu.
  2. Metode doollite, metode ini digunakan untuk mendekomposisi matriks yang menghasilkan elemen diagonla utama matriks segitiga bawah L adalah satu.
  3. Metode Cholesky, metode ini digunakan untuk endekomposisi matriks diagonal utama L dan U sama. Metode ini hanya untuk matriks yang simetris.
  4. Metode operasi elementer, metode ini digunakan untuk mendekomposisi matriks menjadi segitiga atas atau segitiga bawah

Namun, teknik-teknik/metode-metode yang disebutkan diatas tidak akan kita bahas semua, kita hanya akan membahas tentang metode crout dan metode doollite

METODE CROUT

Rumus untuk menyelesaikan persamaan dari elemen matriks segitiga bawah hingga matriks segitiga atas:

METODE DOOLITTLE

Rumus untuk menyelesaikan persamaan dari elemen matriks segitiga atas hingga matriks segitiga bawah:

Contoh 1

Dekomposisi matriks berikut menjadi matriks segitiga bawah (L) dan segitiga atas (U).

Contoh 2

Dekomposisi matriks berikut menjadi matriks segitiga bawah (L) dan segitiga atas (U).


INVERS MATRIKS:


Jika A dan B adalah matriks persegi, dan berlaku A \cdot B = B \cdot A = I maka dikatakan matriks A dan B saling invers. B disebut invers dari A, atau ditulis A^{-1}. Matriks yang mempunyai invers disebut invertible atau matriks non singular, sedangkan matriks yang tidak mempunyai invers disebut matriks singular.
Untuk mencari invers matriks persegi berordo 2×2, coba perhatikan berikut ini.
Jika A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} dengan ad - bc \neq 0, maka invers dari matriks A (ditulis A^{-1}) adalah sebagai berikut:
A^{-1} = \frac {1}{ad - bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}
Jika ad - bc = 0 maka matriks tersebut tidak mempunyai invers, atau disebut matriks singular.
Sifat-sifat matriks persegi yang mempunyai invers:
  • (A \cdot B)^{-1} = B^{-1} \cdot A^{-1}
  • (B \cdot A)^{-1} = A^{-1} \cdot B^{-1}
  • (A^{-1})^t =(A^{t})^{-1}
Contoh: Diketahui A =  dan B = 

Selidiki, apakah A dan B saling invers?

Penyelesaian :

Matriks A dan B saling invers jika berlaku A × B = B × A = I.

A × B = 

B × A = 

Karena A × B = B × A maka A dan B saling invers, dengan A–1 = B dan B–1 = A.



Menentukan Invers Matriks Berordo 2 × 2

Misalkan diketahui matriks A =  , dengan ad – bc ≠ 0.

Suatu matriks lain, misalnya B dikatakan sebagai invers matriks A jika AB = I. Matriks invers dari A ditulis A–1 . Dengan demikian, berlaku :

AA–1 = A–1A = I

Matriks A mempunyai invers jika A adalah matriks nonsingular, yaitu det A ≠ 0. Sebaliknya, jika A matriks singular (det A = 0) maka matriks ini tidak memiliki invers.

Misalkan matriks A =  dan matriks B =  sehingga berlaku A × B = B × A = I. Kita akan mencari elemen-elemen matriks B, yaitu p, q, r, dan s.

Dari persamaan A × B = I, diperoleh :



Jadi, diperoleh sistem persamaan :

ap + br = 1  dan  aq + bs = 0
cp + dr = 0         cq + ds = 1

Dengan menyelesaikan sistem persamaan tersebut, kalian peroleh :
Dengan demikian,
Invers Matriks Berordo 2 × 2
Matriks B memenuhi A × B = I.

Sekarang, akan kita buktikan apakah matriks B × A = I?
persamaan Invers Matriks Berordo 2 × 2
Karena ad – bc ≠ 0, berlaku B × A =  = I

Karena A × B = B × A = I maka B = A–1.

Jadi, jika A =  maka inversnya adalah :


untuk ad – bc ≠ 0.

Contoh Soal 18 :

Tentukan invers matriks-matriks berikut.

a. A = 

b. B = 

Jawaban:
invers matriks

Menentukan Invers Matriks Berordo 3 × 3 

Invers matriks berordo 3 × 3 dapat dicari dengan beberapa cara. Pada pembahasan kali ini kita akan menggunakan cara adjoin dan transformasi baris elementer.

a. Dengan Adjoin

Pada subbab sebelumnya, telah dijelaskan mengenai determinan matriks. Selanjutnya, adjoin A dinotasikan adj (A), yaitu transpose dari matriks yang elemen-elemennya merupakan kofaktor-kofaktor dari elemen-elemen matriks A, yaitu :
adj(A) = (kof(A))T

Adjoin A dirumuskan sebagai berikut.

rumus Adjoin A
Invers matriks persegi berordo 3 × 3 dirumuskan sebagai berikut.


Adapun bukti tentang rumus ini akan kalian pelajari lebih mendalam dijenjang pendidikan yang lebih tinggi.

Contoh Soal 19 :

Diketahui matriks A =  . Tentukan invers matriks A, misalnya kita gunakan perhitungan menurut baris pertama.

Jawaban :

Terlebih dahulu kita hitung determinan A.

det A = 

= 1(1) – 2(2) + 1(1) = –2

Dengan menggunakan rumus adjoin A, diperoleh :

adj(A) = 

Jadi, A–1 dapat dihitung sebagai berikut.
Invers matriks persegi berordo 3 × 3

Bentuk {\displaystyle AI->IA^{-1}}Sunting

A = {\displaystyle {\begin{bmatrix}1&5&5\\-1&-1&0\\2&4&3\\\end{bmatrix}}}
Tentukan Nilai dari A−1
Diawali dengan {\displaystyle \left[{\begin{array}{rrr|rrr}1&5&5&1&0&0\\-1&-1&0&0&1&0\\2&4&3&0&0&1\\\end{array}}\right]}
Operasikan Matriks tersebut
{\displaystyle \left[{\begin{array}{rrr|rrr}1&5&5&1&0&0\\0&4&5&1&1&0\\2&4&3&0&0&1\\\end{array}}\right]} B2 + B1
{\displaystyle \left[{\begin{array}{rrr|rrr}1&5&5&1&0&0\\0&4&5&1&1&0\\0&-6&-7&-2&0&1\\\end{array}}\right]} B3 - 2.B1
{\displaystyle \left[{\begin{array}{rrr|rrr}1&5&5&1&0&0\\0&4&5&1&1&0\\0&0&{\frac {1}{2}}&-{\frac {1}{2}}&{\frac {3}{2}}&1\\\end{array}}\right]} B3 + 3/2.B1
{\displaystyle \left[{\begin{array}{rrr|rrr}1&5&5&1&0&0\\0&1&{\frac {5}{4}}&{\frac {1}{4}}&{\frac {1}{4}}&0\\0&0&1&-1&3&2\\\end{array}}\right]} 1/4.B2, 2.B3
{\displaystyle \left[{\begin{array}{rrr|rrr}1&5&5&1&0&0\\0&1&0&{\frac {3}{2}}&-{\frac {7}{2}}&-{\frac {5}{2}}\\0&0&1&-1&3&2\\\end{array}}\right]} B2 - 5/4.B3
{\displaystyle \left[{\begin{array}{rrr|rrr}1&5&0&6&-15&-10\\0&1&0&{\frac {3}{2}}&-{\frac {7}{2}}&-{\frac {5}{2}}\\0&0&1&-1&3&2\\\end{array}}\right]} B1 - 5.B3
{\displaystyle \left[{\begin{array}{rrr|rrr}1&0&0&-{\frac {3}{2}}&{\frac {5}{2}}&{\frac {5}{2}}\\0&1&0&{\frac {3}{2}}&-{\frac {7}{2}}&-{\frac {5}{2}}\\0&0&1&-1&3&2\\\end{array}}\right]} B1 - 5.B2
{\displaystyle A^{-1}={\begin{bmatrix}-{\frac {3}{2}}&{\frac {5}{2}}&{\frac {5}{2}}\\{\frac {3}{2}}&-{\frac {7}{2}}&-{\frac {5}{2}}\\-1&3&2\\\end{bmatrix}}}


b. Dengan Transformasi Baris Elementer

Untuk menentukan invers matriks An dengan cara transformasi baris elementer, dapat dilakukan dengan langkah-langkah berikut berikut.

1) Bentuklah matriks (An | In), dengan In adalah matriks identitas ordo n.
2) Transformasikan matriks (An | In) ke bentuk (In | Bn), dengan transformasi elemen baris.
3) Hasil dari Langkah 2, diperoleh invers matriks An adalah Bn.
4) Tukarkan 1 baris dengan baris lainnya
5) Letakkan satu baris dengan bilangan bukan nol.
6) Jumlahkan kelipatan suatu baris dengan baris lainnya
   * untuk mencari  b1 >> pecahan dari angka pertama
    * untuk mencari b2,b3 >> lawan dari angka(misalkan positif (+) menjadi negatif (-)

Notasi yang sering digunakan dalam transformasi baris elementer adalah :

a) Bi ↔ Bj : menukar elemen-elemen baris ke-i dengan elemen-elemen baris ke-j;
b) k.Bi : mengalikan elemen-elemen baris ke-i dengan skalar k;
c) Bi + kBj : jumlahkan elemen-elemen baris ke-i dengan k kali elemen-elemen baris ke-j.

Contoh Soal 20 :

Tentukan invers matriks A =  dengan transformasi baris elementer.

Penyelesaian :
invers matriks A dengan transformasi baris elementer

Jadi, diperoleh A–1 = 


Keterangan : 

1/2 B1 : Kalikan elemen-elemen baris ke-1 dengan 1/2.
B2 – 5B1 : Kurangkan baris ke-2 dengan 5 kali elemen-elemen baris ke-1.
B1 – B2 : Kurangi elemen-elemen baris ke-1 dengan elemen-elemen baris ke-2.
2B2 : Kalikan elemen-elemen baris ke-2 dengan 2.

Contoh Soal 21 :

Tentukan invers matriks A =  dengan transformasi baris elementer.

Jawaban :
invers matriks A dengan transformasi baris elementer

Terdapat tiga tipe Operasi Baris Elementer (OBE) dan beberapa sifat determinan matriks. Namun, hanya satu tipe OBE dan dua sifat determinan yang digunakan untuk menghitung determinan matriks.
Jika A adalah matriks segitiga nxn (segitiga atas, segitiga bawah atau segitiga diagonal) maka {\displaystyle det(A)} adalah hasil kali elemen diagonal utama matriks tersebut.
Contoh Soal:
A = {\displaystyle {\begin{bmatrix}1&2&3\\4&5&4\\3&2&1\\\end{bmatrix}}} tentukan determinan A dengan metode OBE!
Jawab:
{\displaystyle {\begin{bmatrix}1&2&3\\0&-3&-8\\0&-4&-8\\\end{bmatrix}}}B2-4B1, B3-3B1
{\displaystyle {\begin{bmatrix}1&2&3\\0&-3&-8\\0&0&8/3\\\end{bmatrix}}}B3-4/3B2
Det(A) = 1x(-3)x(8/3) = -8



Eliminasi Gauss

Eliminasi gauss ditemukan oleh Carl Friedrich Gauss, metode ini dapat dimanfaatkan untuk memecahkan sistem persamaan linear dengan merepresentasikan (mengubah) menjadi bentuk matriks, matriks tersebut lalu diubah kebentuk Eselon Baris melalui Operasi Baris Elementer. Kemudian sistem diselesaikan dengan substitusi balik.

Lalu apa itu eselon baris? dan bagaimana bentuknya?

Bentuk Eselon Baris

Suatu matriks memiliki bentuk eselon baris jika memenuhi 3 kriteria berikut :

  1. Jika didalam baris terdapat elemen-elemen yang tidak semuanya nol, maka bilangan tak nol pertama di dalam baris tersebut adalah 1.

    Contoh : (Perhatikan setiap baris pada matriks berikut)

    \left[\begin{array}{cccc}\color{red}{1}&\color{red}{4}&\color{red}{0}&\color{red}{2}\\\color{blue}{0}&\color{blue}{0}&\color{blue}{-1}&\color{blue}{2}\\\color{green}{0}&\color{green}{0}&\color{green}{0}&\color{green}{1}\end{array}\right]

    Dari matriks diatas baris merah dan baris hijau memenuhi kriteria pertama, karena elemen-elemen pada baris merah atau hijau tidak semuanya nol dan bilangan (elemen) bukan nol pertama (dari kiri) di dalam baris tersebut adalah 1. Sedangkan pada baris biru tidak memenuhi kriteria pertama sebab bilangan (elemen) bukan nol pertama (dari kiri) bukan bernilai 1, melainkan bernilai -1.

  2. Nah kalau ada baris-baris yang semua elemennya  bernilai 0 semua, maka baris-baris tersebut harus dikelompokkan dan diletakkan dibagian bawah matriks.

    Contoh :

    \left[\begin{array}{cccc}\color{red}{0}&\color{red}{0}&\color{red}{0}&\color{red}{0}\\\color{red}{0}&\color{red}{0}&\color{red}{1}&\color{red}{-1}\\\color{red}{0}&\color{red}{0}&\color{red}{0}&\color{red}{0}\end{array}\right],~\left[\begin{array}{ccc}\color{blue}{-2}&\color{blue}{3}&\color{blue}{0}\\\color{blue}{0}&\color{blue}{1}&\color{blue}{-1}\\\color{blue}{0}&\color{blue}{0}&\color{blue}{0}\end{array}\right]

    Dari contoh diatas, matriks dengan elemen berwarna biru memenuhi kriteria kedua sebab terdapat baris yang semua elemennya 0 dan baris tersebut diletakkan di bagian bawah matriks. Sedangkan pada matriks berwarna merah, masih belum memenuhi kriteria kedua, sebab walaupun terdapat baris dengan elemen-elemennya 0, namun baris-baris tersebut tidak dikelompokkan dan tidak diletakkan di bagian bawah matriks tersebut. Pada matriks merah agar memenuhi kriteria kedua seharusnya :

    \left[\begin{array}{cccc}\color{red}{0}&\color{red}{0}&\color{red}{1}&\color{red}{-1}\\\color{red}{0}&\color{red}{0}&\color{red}{0}&\color{red}{0}\\\color{red}{0}&\color{red}{0}&\color{red}{0}&\color{red}{0}\end{array}\right]

  3. Jika terdapat dua baris berurutan yang memenuhi kriteria pertama, maka angka 1 (pertama/utama) dari baris yang lebih rendah berada lebih kekanan dari angka 1(pertama/utama) baris yang diatasnya.

    Contoh :

    \left[\begin{array}{cccc}\color{green}{1}&\color{green}{-2}&\color{green}{1}&\color{green}{2}\\\color{green}{0}&\color{green}{0}&\color{green}{1}&\color{green}{1}\\\color{green}{0}&\color{green}{0}&\color{green}{0}&\color{green}{0}\end{array}\right],~\left[\begin{array}{ccc}\color{blue}{1}&\color{blue}{3}&\color{blue}{0}\\\color{blue}{0}&\color{blue}{1}&\color{blue}{-1}\\\color{blue}{0}&\color{blue}{1}&\color{blue}{-3}\end{array}\right]

    Pada matriks hijau sudah memenuhi kriteria ketiga, karena jelas angka 1 pertama (dari kiri) pada baris yang lebih rendah letaknya lebih kekanan dari angka 1 pertama dari baris yang diatasnya.

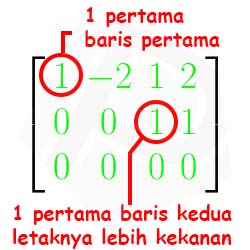
    Syarat Bentuk Eselon Baris

    Sedangkan pada matriks biru belum memenuhi sebab terdapat dua baris berurutan yang melanggar kriteria ketiga yaitu baris ke 2 dan 3. Dimana angka 1 pertama baris ketiga terletak tepat di bawah angka 1 pertama baris kedua.

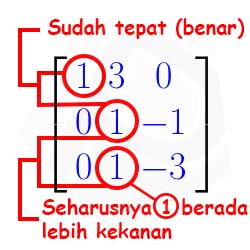
    Syarat Bentuk Eselon Baris

Setelah memahami ketiga kriteria (syarat) dari bentuk eselon baris. Berikut contoh matriks yang mempunyai bentuk eselon baris (memenuhi ketiga kriteria sekaligus).

\left[\begin{array}{ccc}1&-1&2\\0&1&9 \\0&0&1\end{array}\right],~\left[\begin{array}{cccc}1&5&1&0\\0&0&1&0 \\0&0&0&0\end{array}\right],~\left[\begin{array}{ccccc}0&1&2&0&0\\0&0&1&0&0 \\0&0&0&0&1\end{array}\right]

Selanjutnya kita akan menerapkan metode eliminasi gauss dan subtitusi balik untuk memecahkan suatu sistem persamaan linear dengan operasi baris elementer. Disarankan sudah memahami penggunaan operasi baris elementer untuk pemecahan sistem persamaan linear.

Pemecahan SPL dengan Eliminasi Gauss

Ilustrasi Eliminasi Gauss

Gambaran diatas merupakan ilustrasi proses pemecahan Sistem Persamaan Linear (SPL), dimana urutan langkah-langkahnya dinamakan “Eliminasi Gauss” dan operasi yang dilakukan dinamakan “Operasi Baris Elementer (OBE)” dimana eliminasi gauss ini bertujuan membentuk Eselon Baris.

Catatan : Pada proses pemecahan dengan metode eliminasi gauss pada umumnya memiliki macam-macam jalur atau alur operasi yang dilakukan, misalkan pada langkah awal bisa saja kita menemukan beberapa operasi alternatif dan kita bebas memilihnya. Karena terdapat banyak jalur atau alur operasinya maka jika anda mencoba dengan jalur lain (tidak seperti di contoh) kemungkinan anda akan menemukan bentuk sistem/matriks yang berbeda. Namun jangan khawatir selama operasi yang dilakukan menggunakan Operasi Baris Elementer dan dilakukan secara teliti, maka solusi(pemecahan) yang didapat akan sama dan itu merupakan hal yang wajar.

Contoh 1 (Solusi Tunggal)

Diberikan sistem persamaan linear sebagai berikut :

2x+5y+3z =1
3x+4y+2z=-3
x+3y+z=2

Perintah : Tentukan pemecahan sistem persamaan linear di atas dengan  metode eliminasi gauss.

Penyelesaian :

Mula-mula kita representasikan sistem tersebut kedalam bentuk matriks.

\left[{\begin{array}{ccc}2&5&3\\3&4&2\\1&3&1\end{array}}\right|\left.{\begin{array}{c}1\\-3\\2\end{array}}\right]

Langkah 1

Kita akan membuat 1 pertama pada baris pertama dengan beberapa pilihan operasi :

  1. Kita bisa menukar baris ke-1 dengan baris ke-3, dinotasikan R_{1} \leftrightarrow R_{3}
  2. Dengan mengganti baris ke-1 dengan hasil kali baris ke-1 dengan \frac{1}{2} dinotasikan : \frac{1}{2}R_{1} \rightarrow R_{1}

Dari dua pilihan diatas kita bebas memilihnya, namun kita akan menggunakan pilihan yang pertama yaitu R_{1} \leftrightarrow R_{3} sehingga didapat :

\left[{\begin{array}{ccc}2&5&3\\3&4&2\\1&3&1\end{array}}\right|\left.{\begin{array}{c}1\\-3\\2\end{array}}\right]\rightarrow\left[{\begin{array}{ccc}1&3&1\\3&4&2\\2&5&3\end{array}}\right|\left.{\begin{array}{c}2\\-3\\1\end{array}}\right]

Langkah 2

Selanjutnya kita akan menyederhanakan bentuk baris ke-2 dan ke-3 sekaligus yaitu dengan operasi -3R_{1}+R_{2}\leftarrow R_{2} sehingga didapat :

\left[{\begin{array}{ccc}1&3&1\\3&4&2\\2&5&3\end{array}}\right|\left.{\begin{array}{c}2\\-3\\1\end{array}}\right]\rightarrow\left[{\begin{array}{ccc}1&3&1\\0&-5&-1\\2&5&3\end{array}}\right|\left.{\begin{array}{c}2\\-9\\1\end{array}}\right]

Kemudian dilanjut dengan operasi -2R_{1}+R_{3}\rightarrow R_{3}

\left[{\begin{array}{ccc}1&3&1\\0&-5&-1\\2&5&3\end{array}}\right|\left.{\begin{array}{c}2\\-9\\1\end{array}}\right]\rightarrow\left[{\begin{array}{ccc}1&3&1\\0&-5&-1\\0&-1&1\end{array}}\right|\left.{\begin{array}{c}2\\-9\\-3\end{array}}\right]

Langkah 3

Kita akan membuat 1 pertama pada baris kedua dengan operasi -6R_{3}+R_{2}\rightarrow R_{2} dan diperoleh :

\left[{\begin{array}{ccc}1&3&1\\0&-5&-1\\0&-1&1\end{array}}\right|\left.{\begin{array}{c}2\\-9\\-3\end{array}}\right]\rightarrow\left[{\begin{array}{ccc}1&3&1\\0&1&-7\\0&-1&1\end{array}}\right|\left.{\begin{array}{c}2\\9\\-3\end{array}}\right]

Langkah 4

Kita akan menyederhanakan lagi baris ke-3 dengan operasi 1R_{2}+R_{3}\rightarrow R_{3}

\left[{\begin{array}{ccc}1&3&1\\0&1&-7\\0&-1&1\end{array}}\right|\left.{\begin{array}{c}2\\9\\-3\end{array}}\right]\rightarrow\left[{\begin{array}{ccc}1&3&1\\0&1&-7\\0&0&-6\end{array}}\right|\left.{\begin{array}{c}2\\9\\6\end{array}}\right]

Langkah 5

Selanjutnya kita akan membentuk 1 pertama pada baris ke-3 dengan operasi -\frac{1}{6}R_{3}\rightarrow R_{3}

\left[{\begin{array}{ccc}1&3&1\\0&1&-7\\0&0&-6\end{array}}\right|\left.{\begin{array}{c}2\\9\\6\end{array}}\right]\rightarrow\left[{\begin{array}{ccc}1&3&1\\0&1&-7\\0&0&1\end{array}}\right|\left.{\begin{array}{c}2\\9\\-1\end{array}}\right]

Dari matriks terakhir tersebut sudah memenuhi ketiga kriteria bentuk eselon baris. Selanjutnya tinggal mengubahnya kembali menjadi sistem persamaan linear :

\left[{\begin{array}{ccc}1&3&1\\0&1&-7\\0&0&1\end{array}}\right|\left.{\begin{array}{c}2\\9\\-1\end{array}}\right]\rightarrow \begin{array}{c}x+3y+z=2\dots\text{(1)}\\y-7z=9\dots\text{(2)}\\z=-1\dots\text{(3)}\end{array}

Kita dapat memulai dengan mensubstitusikan persamaan (3) ke persamaan (2) sehingga didapat :

y-7z=9

\Leftrightarrow y=9+7z=9+7(-1)=2

Kemudian nilai dari y dan z juga kita substitusikan ke persamaan (1) dan kita dapatkan :

x+3y+z=2

\Leftrightarrow x=2-3y-z

\Leftrightarrow x=2-3(2)-(-1)=-3

Jadi didapat solusi tunggal yaitu x=-3, y=2 dan z=-1.

Contoh 2 (Banyak Solusi)

Diberikan sistem persamaan linear sebagai berikut :

2x+10y+4z =-2
x+4y+5z=-3
3x+15y+6z=-3

Perintah : Tentukan pemecahan sistem persamaan linear di atas dengan  metode eliminasi gauss.

Penyelesaian :

Kita representasikan kedalam bentuk matriks :

\left[{\begin{array}{ccc}2&10&4\\1&4&5\\3&15&6\end{array}}\right|\left.{\begin{array}{c}-2\\-3\\-3\end{array}}\right]

Langkah 1

Kita buat 1 pertama pada baris pertama dengan pilihan :

  1. Dengan menukar baris ke-1 dengan baris ke-2, dinotasikan : R_{1} \leftrightarrow R_{2}
  2. Dengan mengganti baris ke-1 dengan hasil kali baris ke-1 dengan \frac{1}{2}, dinotasikan : \frac{1}{2}R_{1} \rightarrow R_{1}

Kita pilih opsi kedua yaitu menggunakan operasi \frac{1}{2}R_{1} \rightarrow R_{1} sehingga kita peroleh :

\left[{\begin{array}{ccc}2&10&4\\1&4&5\\3&15&6\end{array}}\right|\left.{\begin{array}{c}-2\\-3\\-3\end{array}}\right]\rightarrow\left[{\begin{array}{ccc}1&5&2\\1&4&5\\3&15&6\end{array}}\right|\left.{\begin{array}{c}-1\\-3\\-3\end{array}}\right]

Langkah 2

Kita sederhanakan baris ke-2 dengan operasi -1R_{1}+R_{2}\rightarrow R_{2}

\left[{\begin{array}{ccc}1&5&2\\1&4&5\\3&15&6\end{array}}\right|\left.{\begin{array}{c}-1\\-3\\-3\end{array}}\right]\rightarrow\left[{\begin{array}{ccc}1&5&2\\0&-1&3\\3&15&6\end{array}}\right|\left.{\begin{array}{c}-1\\-2\\-3\end{array}}\right]

Dilanjut penyederhanaan baris ke-3 dengan operasi -3R_{1}+R_{3}\rightarrow R_{3}

\left[{\begin{array}{ccc}1&5&2\\0&-1&3\\3&15&6\end{array}}\right|\left.{\begin{array}{c}-1\\-2\\-3\end{array}}\right]\rightarrow \left[{\begin{array}{ccc}1&5&2\\0&-1&3\\0&0&0\end{array}}\right|\left.{\begin{array}{c}-1\\-2\\0\end{array}}\right]

Langkah 3

Kita buat 1 pertama pada baris ke-2 dengan operasi -1R_{2}\rightarrow R_{2}

\left[{\begin{array}{ccc}1&5&2\\0&-1&3\\0&0&0\end{array}}\right|\left.{\begin{array}{c}-1\\-2\\0\end{array}}\right]\rightarrow \left[{\begin{array}{ccc}1&5&2\\0&1&-3\\0&0&0\end{array}}\right|\left.{\begin{array}{c}-1\\2\\0\end{array}}\right]

Matriks terakhir sudah memenuhi bentuk eselon baris sehingga selanjutnya menggunakan metode substitusi balik, namun sebelumnya kita harus mengubahnya kembali menjadi bentuk sistem persamaan linear.

\left[{\begin{array}{ccc}1&5&2\\0&1&-3\\0&0&0\end{array}}\right|\left.{\begin{array}{c}-1\\2\\0\end{array}}\right]\rightarrow\begin{array}{c}x+5y+2z=-1\dots(1)\\y-3z=2\dots(2)\end{array}

Perhatikan persamaan (2) :

y-3z=2\Leftrightarrow y=2+3z

Subtitusikan ke persamaan (1) dan diperoleh :

x+5y+2z=-1

\Leftrightarrow x=-1-5y-2z

\Leftrightarrow x=-1-5(2+3z)-2z

\Leftrightarrow x=-1-10-15z-2z

\Leftrightarrow x=-11-17z

Jelaslah pemecahannya banyak karena nilai dari z sendiri mempunyai tak terhingga banyaknya kemungkinan. Jadi himpunan penyelesaiannya yaitu :

\text{HP}=\{(x,y,z)\mid x=-11-17z,~y=2+3z,~\forall~\text{sebarang bilangan}~z\}

Contoh 3 (Tidak Punya Solusi)

Diberikan sistem persamaan linear sebagai berikut :

3x+12y+15z=6
2x+8y+10z=-6
4x+5y-6z =-2

Perintah : Tentukan pemecahan (bila ada) dari sistem persamaan linear di atas dengan  metode eliminasi gauss.

Penyelesaian :

Seperti biasa kita representasikan dulu ke dalam bentuk matriks.

\left[{\begin{array}{ccc}3&12&15\\2&8&10\\4&5&-6\end{array}}\right|\left.{\begin{array}{c}6\\-6\\-2\end{array}}\right]

Langkah 1

Kita buat 1 pertama pada baris pertama dengan operasi \frac{1}{3}R_{1} \rightarrow R_{1}

\left[{\begin{array}{ccc}3&12&15\\2&8&10\\4&5&-6\end{array}}\right|\left.{\begin{array}{c}6\\-6\\-2\end{array}}\right]\rightarrow\left[{\begin{array}{ccc}1&4&5\\2&8&10\\4&5&-6\end{array}}\right|\left.{\begin{array}{c}2\\-6\\-2\end{array}}\right]

Langkah 2

Selanjutnya kita sederhanakan baris ke-2 dengan operasi -2R_{1}+R_{2}\rightarrow R_{2} dan diperoleh :

\left[{\begin{array}{ccc}1&4&5\\2&8&10\\4&5&-6\end{array}}\right|\left.{\begin{array}{c}2\\-6\\-2\end{array}}\right]\rightarrow\left[{\begin{array}{ccc}1&4&5\\0&0&0\\4&5&-6\end{array}}\right|\left.{\begin{array}{c}2\\-10\\-2\end{array}}\right]

Perhatikan matriks terakhir diatas, kita coba ubah kembali menjadi bentuk sistem persamaan linear.

\left[{\begin{array}{ccc}1&4&5\\0&0&0\\4&5&-6\end{array}}\right|\left.{\begin{array}{c}2\\-10\\-2\end{array}}\right]\rightarrow\begin{array}{c}x+4y+5z=2\dots(1)\\(0)x+(0)y+(0)z=-10\dots(2)\\4x+5y-6z=-2\dots(3)\end{array}

Kita tahu untuk sembarang bilangan x, y, z bila dikalikan 0 akan menghasilkan 0 sehingga :

(0)x+(0)y+(0)z =0



Eliminasi Gauss-Jordan

Eliminasi Gauss-Jordan adalah prosedur pemecahan sistem persamaan linear dengan mengubahnya menjadi bentuk matriks eselon baris tereduksi dengan Operasi Baris Elementer.

Perhatikan ilutrasi berikut :

Ilustrasi Eliminasi Gauss Jordan

Lalu apa itu eselon baris tereduksi?

Bentuk Eselon Baris Tereduksi

Matriks Eselon Baris Tereduksi adalah sebuah bentuk matriks eselon baris yang lebih disederhanakan yang bertujuan agar lebih mudah dalam pencarian pemecahan (solusi) dari suatu sistem persamaan .

Agar mencapai bentuk eselon baris tereduksi diperlukan 4 sifat yang terdiri 3 sifat bentuk eselon baris dan 1 sifat khusus.

Berikut 4 sifat agar terbentuk eselon baris tereduksi :

  1. Jika suatu baris yang semua elemennya tidak nol semua, maka bilangan tidak nol pertama dalam baris tersebut adalah 1. Bisa kita sebut dengan 1 utama/pertama.
  2. Jika terdapat baris yang semuanya elemennya bernilai nol, maka semua baris yang seperti itu harus dikelompokkan dan diletakkan  di bawah matriks.
  3. Setiap dua baris yang berurutan yang memenuhi sifat ke-1, maka 1 utama dalam baris yang lebih rendah letaknya harus lebih kekanan dari 1 utama dalam baris yang lebih tinggi.

    Berikut contoh matriks eselon baris yang memenuhi ketiga sifat di atas :

    A=\left[{\begin{array}{ccccc}0&1&0&0&5\\0&0&1&0&0\\0&0&0&0&1\end{array}}\right],~B=\left[{\begin{array}{ccc}1&2&3\\0&1&-2\end{array}}\right],~C=\left[{\begin{array}{cc}1&-1\\0&1\end{array}}\right]

    Di materi sebelumnya tentang eliminasi gauss sudah dijelaskan secara lebih jelas dan runtut mengenai Bentuk Eselon Baris (3 sifat diatas) dan disertai contoh yang menarik. Jadi disarankan membaca dulu materi tentang Eliminasi Gauss.

  4. Sifat ke-4 ini merupakan sifat khusus yaitu setiap kolom yang mengandung 1 utama maka elemen-elemen lain selain 1 utama bernilai nol.

    Berikut contoh matriks eselon baris tereduksi yang memenuhi keempat syarat di atas :

    A=\left[{\begin{array}{cccc}0&\color{red}{1}&1&\color{blue}{0}\\0&\color{red}{0}&0&\color{blue}{1}\\0&\color{red}{0}&0&\color{blue}{0}\end{array}}\right],~B=\left[{\begin{array}{ccc}\color{red}{1}&\color{blue}{0}&\color{green}{0}\\\color{red}{0}&\color{blue}{1}&\color{green}{0}\\\color{red}{0}&\color{blue}{0}&\color{green}{1}\end{array}}\right],~C=\left[{\begin{array}{cc}0&0\\0&0\end{array}}\right]

Setelah memahami bentuk eselon baris tereduksi selanjutnya kita akan mencoba memecahkan sistem persamaan linear dengan eliminasi gauss-jordan yakni dengan cara merepresentasikan kedalam  matriks kemudian mengubahnya kebentuk eselon baris tereduksi.

Penerapan Eliminasi Gauss-Jordan

Eliminasi gauss-jordan akan lebih terasa bermanfaat jika sistem persamaan linear tersebut terdiri dari banyak persamaan dan variabel, semisal sistem tersebut mempunyai 5 persamaan dan 5 variabel di dalamnya. Selain itu, eliminasi gauss dan eliminasi gauss-jordan juga dapat diterapkan pada sistem persamaan taklinear tertentu (lihat pada contoh ke-2).

Sebenarnya pemecahan SPL dengan metode eliminasi gauss-jordan sudah diterapkan pada postingan sebelumnnya, yaitu pada materi Pemecahan SPL dengan Operasi Baris Elementer yang mana terdapat 3 contoh unik (solusi tunggal, banyak solusi dan tidak punya solusi). Ketiga contoh tersebut dikerjakan dengan prosedur eliminasi gauss-jordan yang dilakukan secara jelas dan runtut.

Sehingga sekarang agar lebih menarik kita akan mencoba variasi soal yang lebih unik.

Contoh 1 (Linear)

Diberikan sistem persamaan linear sebagai berikut :

x+2y-3z=4
3x-y+5z=2
4x+y+(k^2 -14)z=k+2

Tentukan nilai k agar SPL di atas :

  1. Tidak mempunyai penyelesaian;
  2. Tepat mempunyai satu penyelesaian;
  3. Mempunyai tak hingga banyak penyelesaian;

Penyelesaian :

Pertama kita representasikan sistem persamaan linear tersebut kedalam bentuk matriks :

\left[{\begin{array}{ccc}1&2&-3\\3&-1&5\\4&1&k^2 – 14\end{array}}\right|\left.{\begin{array}{c}4\\2\\k+2\end{array}}\right]

Langkah 1

Karena pada baris pertama sudah terdapat 1 utama, kita akan menyederhanakan baris ke-2 dengan operasi -3R_{1}+R_{2}\rightarrow R_{2}, sehingga diperoleh :

\left[{\begin{array}{ccc}1&2&-3\\3&-1&5\\4&1&k^2 – 14\end{array}}\right|\left.{\begin{array}{c}4\\2\\k+2\end{array}}\right]\rightarrow \left[{\begin{array}{ccc}1&2&-3\\0&-7&14\\4&1&k^2 – 14\end{array}}\right|\left.{\begin{array}{c}4\\-10\\k+2\end{array}}\right]

Kemudian dilanjut penyederhanaan pada baris ke-3 dengan operasi -4R_{1}+R_{3}\rightarrow R_{3}, didapat :

\left[{\begin{array}{ccc}1&2&-3\\0&-7&14\\4&1&k^2 – 14\end{array}}\right|\left.{\begin{array}{c}4\\-10\\k+2\end{array}}\right]\rightarrow \left[{\begin{array}{ccc}1&2&-3\\0&-7&14\\0&-7&k^2 – 2\end{array}}\right|\left.{\begin{array}{c}4\\-10\\k-14\end{array}}\right]

Langkah 2

Kita buat 1 utama pada baris ke-2 dengan operasi -\frac{1}{7}R_{2} \rightarrow R_{2} dan kita peroleh :

\left[{\begin{array}{ccc}1&2&-3\\0&-7&14\\0&-7&k^2 – 2\end{array}}\right|\left.{\begin{array}{c}4\\-10\\k-14\end{array}}\right]\rightarrow \left[{\begin{array}{ccc}1&2&-3\\0&1&-2\\0&-7&k^2 – 2\end{array}}\right|\left.{\begin{array}{c}4\\\frac{10}{7}\\k-14\end{array}}\right]

Selanjutnya kita sederhanakan baris ke-3 dengan operasi 7R_{2} +R_{3}\rightarrow R_{3}

\left[{\begin{array}{ccc}1&2&-3\\0&1&-2\\0&-7&k^2 – 2\end{array}}\right|\left.{\begin{array}{c}4\\\frac{10}{7}\\k-14\end{array}}\right]\rightarrow \left[{\begin{array}{ccc}1&2&-3\\0&1&-2\\0&0&k^2 – 16\end{array}}\right|\left.{\begin{array}{c}4\\\frac{10}{7}\\k-4\end{array}}\right]

Langkah 3

Karena tujuan kita akan mengidentifikasi nilai k, maka kita cukup fokus pada baris ke-3. apabila diubah kembali kedalam bentuk sistem persamaan linear maka :

\left[{\begin{array}{ccc}1&2&-3\\0&1&-2\\0&0&k^2 – 16\end{array}}\right|\left.{\begin{array}{c}4\\\frac{10}{7}\\k-4\end{array}}\right]\rightarrow \begin{array}{c}x+2y-3z=4\\y-2z=\frac{10}{7}\\(k^2 -16)z=k-4\end{array}

Perhatikan pada persamaan ketiga :

(k^2 – 16)z = k-4

\Leftrightarrow (k-4)(k+4)z=k-4

\Leftrightarrow (k-4)(k+4)z -(k-4)=0

\Leftrightarrow (k-4)((k+4)z -1)=0

Kita bagi menjadi 2 kasus :

Kasus 1

Jika k-4=0 atau k=4 maka jika disubstitusikan ke persamaan ke-3 diperoleh :

0(8z-1)=0

Mengingat sifat sembarang bilangan jika dikalikan nol akan bernilai nol maka nilai dari 8z-1 mempunyai tak hingga kemungkinan. Dapat dimisalkan n=8z-1 atau 8z=n+1\Leftrightarrow z=\frac{n+1}{8} untuk sembarang bilangan n. Akibatnya sistem persamaan linear tersebut mempunyai tak hingga banyaknya penyelesaian.

Kasus 2

Jika (k+4)z-1= 0 maka :

(k+4)z =1

\Leftrightarrow z=\frac{1}{k+4},~\text{dengan}~k\neq -4

Dari persamaan di atas, sistem tersebut akan konsisten (mempunyai solusi baik tunggal ataupun banyak) jika nilai dari k \neq -4. Dari pernyataan-pernyataan di atas dan sebelumnya, jika kita menginginkan sistem tersebut mempunyai solusi tunggal maka haruslah k\neq \{-4,4\}. Sedangkan jika menginginkan sistem tersebut tidak mempunyai solusi maka haruslah k=-4.

Kesimpulan

  1. SPL tersebut akan tidak mempunyai solusi jika k=-4
  2. SPL tersebut akan mempunyai tak hingga solusi jika k=4
  3. SPL tersebut akan mempunyai solusi tunggal jika k\neq \{-4,4\}

Contoh 2 (Tak Linear)

Untuk membedakan sistem persamaan linear dengan sistem persamaan tak linear, bisa baca kembali Penjelasan Mengenai SIstem Persamaan Linear.

Tentukan pemecahan sistem persamaan tak linear untuk sudut-sudut yang tak diketahui \alpha, \beta, \gamma

2\sin{\alpha} – \cos{\beta} + 3\tan{\gamma} = 3
4\sin{\alpha} + 2\cos{\beta} – 2\tan{\gamma} = 2
6\sin{\alpha} – 3\cos{\beta} + \tan{\gamma} = 9

Dengan 0 \leq \alpha \leq 2\pi,~0 \leq \beta \leq 2\pi, dan 0 \leq \gamma < \pi,~.

Penyelesaian :

Kalau kita perhatikan bentuk sistem persamaan tak linear di atas tidak beda jauh dengan sistem persamaan linear yang biasa kita kenal, sehingga jika kita representasikan kedalam bentuk matriks akan diperoleh :

\left[{\begin{array}{ccc}2&-1&3\\4&2&-2\\6&-3&1\end{array}}\right|\left.{\begin{array}{c}3\\2\\9\end{array}}\right]

Kita akan menggunakan eliminasi gauss-jordan untuk memecahkan sistem tersebut.

Langkah 1

Kita buat 1 utama pada baris pertama dengan operasi \frac{1}{2}R_{1} \rightarrow R_{1} sehingga didapat :

\left[{\begin{array}{ccc}2&-1&3\\4&2&-2\\6&-3&1\end{array}}\right|\left.{\begin{array}{c}3\\2\\9\end{array}}\right]\rightarrow \left[{\begin{array}{ccc}1&-\frac{1}{2}&\frac{3}{2}\\4&2&-2\\6&-3&1\end{array}}\right|\left.{\begin{array}{c}\frac{3}{2}\\2\\9\end{array}}\right]

Langkah 2

Kita sederhanakan baris ke-2 dengan operasi -4R_{1} +R_{2} \rightarrow R_{2}

\left[{\begin{array}{ccc}1&-\frac{1}{2}&\frac{3}{2}\\4&2&-2\\6&-3&1\end{array}}\right|\left.{\begin{array}{c}\frac{3}{2}\\2\\9\end{array}}\right]\rightarrow \left[{\begin{array}{ccc}1&-\frac{1}{2}&\frac{3}{2}\\0&4&-8\\6&-3&1\end{array}}\right|\left.{\begin{array}{c}\frac{3}{2}\\-4\\9\end{array}}\right]

Kemudian kita sederhanakan juga baris ke-3 dengan operasi -6R_{1} +R_{3} \rightarrow R_{3}

\left[{\begin{array}{ccc}1&-\frac{1}{2}&\frac{3}{2}\\0&4&-8\\6&-3&1\end{array}}\right|\left.{\begin{array}{c}\frac{3}{2}\\-4\\9\end{array}}\right]\rightarrow \left[{\begin{array}{ccc}1&-\frac{1}{2}&\frac{3}{2}\\0&4&-8\\0&0&-8\end{array}}\right|\left.{\begin{array}{c}\frac{3}{2}\\-4\\0\end{array}}\right]

Langkah 3

Kita buat 1 utama untuk baris ke-2 dengan cara menggunakan operasi \frac{1}{4}R_{2}\rightarrow R_{2}

\left[{\begin{array}{ccc}1&-\frac{1}{2}&\frac{3}{2}\\0&4&-8\\0&0&-8\end{array}}\right|\left.{\begin{array}{c}\frac{3}{2}\\-4\\0\end{array}}\right]\rightarrow \left[{\begin{array}{ccc}1&-\frac{1}{2}&\frac{3}{2}\\0&1&-2\\0&0&-8\end{array}}\right|\left.{\begin{array}{c}\frac{3}{2}\\-1\\0\end{array}}\right]

Sekalian kita buat 1 utama dengan operasi -\frac{1}{8}R_{3} \rightarrow R_{3}

\left[{\begin{array}{ccc}1&-\frac{1}{2}&\frac{3}{2}\\0&1&-2\\0&0&-8\end{array}}\right|\left.{\begin{array}{c}\frac{3}{2}\\-1\\0\end{array}}\right]\rightarrow \left[{\begin{array}{ccc}1&-\frac{1}{2}&\frac{3}{2}\\0&1&-2\\0&0&1\end{array}}\right|\left.{\begin{array}{c}\frac{3}{2}\\-1\\0\end{array}}\right]

Langkah 4

Jika kita perhatikan bentuk terakhir matriks di atas sudah memenuhi bentuk eselon baris, selanjutnya kita akan mengubahnya menjadi eselon baris tereduksi.

Kita sederhanakan lagi baris ke-1 dengan operasi \frac{1}{2}R_{2}+R_{1} \rightarrow R_{1}

\left[{\begin{array}{ccc}1&-\frac{1}{2}&\frac{3}{2}\\0&1&-2\\0&0&1\end{array}}\right|\left.{\begin{array}{c}\frac{3}{2}\\-1\\0\end{array}}\right]\rightarrow \left[{\begin{array}{ccc}1&0&\frac{1}{2}\\0&1&-2\\0&0&1\end{array}}\right|\left.{\begin{array}{c}1\\-1\\0\end{array}}\right]

Dilanjut dengan operasi -\frac{1}{2}R_{3} +R_{1} \rightarrow R_{1}

\left[{\begin{array}{ccc}1&0&\frac{1}{2}\\0&1&-2\\0&0&1\end{array}}\right|\left.{\begin{array}{c}1\\-1\\0\end{array}}\right] \rightarrow \left[{\begin{array}{ccc}1&0&0\\0&1&-2\\0&0&1\end{array}}\right|\left.{\begin{array}{c}1\\-1\\0\end{array}}\right]

Begitu pula untuk baris ke-2 kita sederhanakan lagi dengan operasi 2R_{3} +R_{2} \rightarrow R_{2} sehingga diperoleh :

\left[{\begin{array}{ccc}1&0&0\\0&1&-2\\0&0&1\end{array}}\right|\left.{\begin{array}{c}1\\-1\\0\end{array}}\right] \rightarrow \left[{\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}}\right|\left.{\begin{array}{c}1\\-1\\0\end{array}}\right]

Bentuk terkahir sudah memenuhi bentuk eselon tereduksi, kemudian selanjutnya kita nyatakan kembali kedalam sistem persamaan tak linear sebagai berikut.

\left[{\begin{array}{ccc}1&0&0\\0&1&-2\\0&0&1\end{array}}\right|\left.{\begin{array}{c}1\\-1\\0\end{array}}\right] \rightarrow \begin{array}{c}\sin{\alpha}=1\\\cos{\beta}=-1\\\tan{\gamma}=0\end{array}

Untuk persamaan pertama :

\sin{\alpha}=1

Dengan 0\leq \alpha \leq 2\pi, maka nilai \alpha yang memenuhi adalah \alpha = 90^{\circ}. Sedangkan untuk persamaan \cos{\beta}=-1 dan \tan{\gamma}=0 nilai \beta dan \gamma yang memenuhi yaitu berturut-turut 180^{\circ} dan 0^{\circ}mengingat 0 \leq \beta \leq 2\pi,~0 \leq \gamma < \pi.



Aturan Cramer untuk Sistem 3 × 3

Aturan Cramer dapat diperluas untuk sistem persamaan linear 3 × 3, dengan menggunakan pola yang sama dengan sistem 2 × 2. Diberikan sistem umum 3 × 3,

Sistem 3 x 3

Solusi-solusi dari sistem tersebut adalah x = Dx/D, y = Dy/D, dan z = Dz/D, dimana Dx, Dy, dan Dz dibentuk dengan mengganti koefisien variable-variabel yang bersangkutan dengan konstanta, dan D adalah determinan dari matriks koefisien (D ≠ 0).

Penerapan Aturan Cramer untuk Sistem 3 × 3

Diberikan suatu sistem persamaan linear 3 × 3

Sistem 3 x 3 Rumus

Solusi dari sistem tersebut adalah (x, y, z), dimana

x, y, z

dengan syarat D ≠ 0.

Contoh 2: Menyelesaikan Sistem 3 × 3 Menggunakan Aturan Cramer

Selesaikan sistem berikut dengan menggunakan aturan Cramer.

Contoh 2

Pembahasan Pertama kita tentukan determinan dari matriks koefisien untuk memastikan apakah aturan Cramer dapat diterapkan atau tidak. Dengan menggunakan baris ketiga kita mendapatkan

Contoh 2 D

Karena D ≠ 0, kita lanjut untuk menentukan determinan dari matriks-matriks lainnya dengan menggunakan Ms. Excel (rumus untuk menentukan determinan dalam Ms. Excel adalah “=MDETERM(array)”).

Contoh 2 Dx, Dy, Dz

Sehingga kita memperoleh,

Contoh 2 x, y, z

Jadi, selesaian dari sistem tersebut adalah (2, 0, –1). Selesaian ini dapat diuji ke dalam sistem yang diberikan. Semoga bermanfaat, yos3prens.


Komentar

Posting Komentar

Postingan Populer